Loading [MathJax]/jax/output/HTML-CSS/config.js
full
search.png

Search

close.png

Cancel

Volume 41, Issue 1
The $H^p-H^q$ Estimates for a Class of Dispersive Equations with Finite Type Geometry

Qingquan Deng & Xuejian Meng

DOI: 10.4208/aam.OA-2025-0001

Ann. Appl. Math., 41 (2025), pp. 77-111.

Published online: 2025-04

Preview Full PDF 84 1256

Cited by

google scholar semantic scholar
Export citation
  • Abstract

This paper studies the $H^p-H^q$ estimates of a class of oscillatory integrals related to dispersive equations

image.png

under the assumption that the level hypersurfaces are convex and of finite type. As applications, we obtain the decay estimates for the solutions of higher order homogeneous and inhomogeneous Schrödinger equations.

  • Keywords

Dispersive equations, $H^p-H^q$ estimates, finite type geometry, decay estimates.

  • AMS Subject Headings

42B30, 42B37

  • Copyright

COPYRIGHT: © Global Science Press

  • Email address
  • BibTex
  • RIS
  • TXT
@Article{AAM-41-77, author = {Deng , Qingquan and Meng , Xuejian}, title = {The $H^p-H^q$ Estimates for a Class of Dispersive Equations with Finite Type Geometry}, journal = {Annals of Applied Mathematics}, year = {2025}, volume = {41}, number = {1}, pages = {77--111}, abstract = {

This paper studies the $H^p-H^q$ estimates of a class of oscillatory integrals related to dispersive equations

image.png

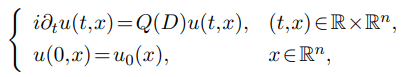
under the assumption that the level hypersurfaces are convex and of finite type. As applications, we obtain the decay estimates for the solutions of higher order homogeneous and inhomogeneous Schrödinger equations.

}, issn = {}, doi = {https://doi.org/10.4208/aam.OA-2025-0001}, url = {http://global-sci.org/intro/article_detail/aam/23963.html} }
TY - JOUR T1 - The $H^p-H^q$ Estimates for a Class of Dispersive Equations with Finite Type Geometry AU - Deng , Qingquan AU - Meng , Xuejian JO - Annals of Applied Mathematics VL - 1 SP - 77 EP - 111 PY - 2025 DA - 2025/04 SN - 41 DO - http://doi.org/10.4208/aam.OA-2025-0001 UR - https://global-sci.org/intro/article_detail/aam/23963.html KW - Dispersive equations, $H^p-H^q$ estimates, finite type geometry, decay estimates. AB -

This paper studies the $H^p-H^q$ estimates of a class of oscillatory integrals related to dispersive equations

image.png

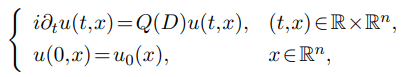
under the assumption that the level hypersurfaces are convex and of finite type. As applications, we obtain the decay estimates for the solutions of higher order homogeneous and inhomogeneous Schrödinger equations.

Deng , Qingquan and Meng , Xuejian. (2025). The $H^p-H^q$ Estimates for a Class of Dispersive Equations with Finite Type Geometry. Annals of Applied Mathematics. 41 (1). 77-111. doi:10.4208/aam.OA-2025-0001
Copy to clipboard
BibteX RIS TXT
The citation has been copied to your clipboard