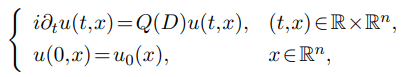@Article{AAM-41-77,
author = {Deng , Qingquan and Meng , Xuejian},
title = {The $H^p-H^q$ Estimates for a Class of Dispersive Equations with Finite Type Geometry},
journal = {Annals of Applied Mathematics},
year = {2025},
volume = {41},
number = {1},
pages = {77--111},
abstract = {<p style="text-align: justify;">This paper studies the $H^p-H^q$ estimates of a class of oscillatory
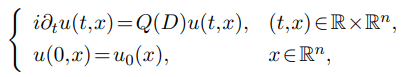
integrals related to dispersive equations<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20250415/1744706566710226.png" title="1744706566710226.png" alt="image.png"/></p><p style="text-align: justify;">under the assumption that the level hypersurfaces are convex and of finite type.
As applications, we obtain the decay estimates for the solutions of higher order
homogeneous and inhomogeneous Schrödinger equations.<br/></p>},
issn = {},
doi = {https://doi.org/10.4208/aam.OA-2025-0001},
url = {http://global-sci.org/intro/article_detail/aam/23963.html}
}