The time-space nonlocal evolution equations are powerful implementation for modeling anomalous diffusion. In this research, we study the nonlocal nonautonomous reaction-diffusion equation

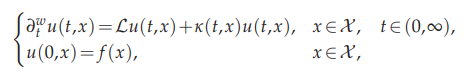
where $\chi$ is a Lusin space, $∂^w_t$ is a generalized time fractional derivative, $κ$ is a bounded reaction rate, and $\mathcal{L}$ is an infinitesimal generator in terms of semigroup induced by a symmetric Markov process $X.$ We show that the stochastic representation $u(t,x)$ defined by $$u(t,x)=\mathbb{E}^x[e^{\int^t_0\kappa(r,X_{E_t-E_r})dE_r}f(X_{E_t})]$$ is the unique mild as well as weak solution. By further analysis, one can get that the above stochastic representation is also the unique strong solution, and the higher spatial and temporal regularity are obtained. In some particular cases, the corresponding dynamical behaviors are displayed.