TY - JOUR
T1 - Blowing Up Solutions to Slightly Sub- or Super-Critical Lane-Emden Systems with Neumann Boundary Conditions
AU - Guo , Qing
AU - Liu , Junyuan
JO - Analysis in Theory and Applications
VL - 1
SP - 1
EP - 34
PY - 2025
DA - 2025/04
SN - 41
DO - http://doi.org/10.4208/ata.OA-0026
UR - https://global-sci.org/intro/article_detail/ata/23956.html
KW - Lane-Emden system, Neumann problem, blow up solutions, reduction method.
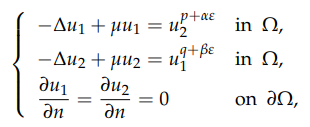
AB - <p style="text-align: justify;">We prove that, for some suitable smooth bounded domain, there exists a
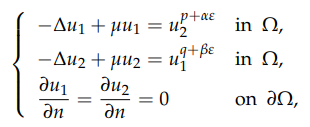
solution to the following Neumann problem for the Lane-Emden system:<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20250411/1744361277620882.png" title="1744361277620882.png" alt="image.png" width="297" height="124"/></p><p style="text-align: justify;">where $Ω$ is some smooth bounded domain in $\mathbb{R}^N,$ $N ≥ 4,$ $\mu &gt; 0,$ $α &gt; 0,$ $β &gt; 0$ are
constants and $ε\ne 0$ is a small number. We show that there exists a solution to the
slightly supercritical problem for $ε &gt; 0,$ and for $ε &lt; 0,$ there also exists a solution to the
slightly subcritical problem if the domain is not convex.<br/>Comparing with the single elliptic equations, the challenges and novelty are manifested in the construction of good approximate solutions characterizing the boundary
behavior under Neumann boundary conditions, in which process, the selection of the
range of nonlinear coupling exponents and the weighted Sobolev spaces requires elaborate discussion.<br/></p>