@Article{JPDE-38-61,
author = {He , QihanLi , Yafei and Peng , Yanfang},
title = {Ground State Solutions to a Coupled Nonlinear Logarithmic Hartree System},
journal = {Journal of Partial Differential Equations},
year = {2025},
volume = {38},
number = {1},
pages = {61--79},
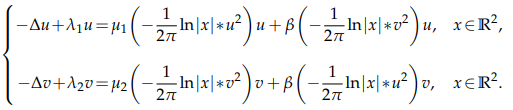
abstract = {<p style="text-align: justify;">In this paper, we study the following coupled nonlinear logarithmic Hartree
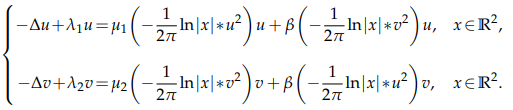
system<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20250408/1744100193327310.png" title="1744100193327310.png" alt="image.png"/></p><p style="text-align: justify;">where $β,\mu_i,λ_i$ ($i=1,2$) are positive constants, ∗ denotes the convolution in $\mathbb{R}^2.$ By
considering the constraint minimum problem on the Nehari manifold, we prove the
existence of ground state solutions for $β &gt; 0$ large enough. Moreover, we also show
that every positive solution is radially symmetric and decays exponentially.<br/></p>},
issn = {2079-732X},
doi = {https://doi.org/10.4208/jpde.v38.n1.4},
url = {http://global-sci.org/intro/article_detail/jpde/23952.html}
}